Rank Deficient Models

STA 721: Lecture 3

Merlise Clyde (clyde@duke.edu)

Duke University

Outline

Rank Deficient Models
Generalized Inverses, Projections and MLEs/OLS
Class of Unbiased Estimators

Readings: - Christensen Chapter 2 and Appendix B - Seber & Lee Chapter 3

Geometric View

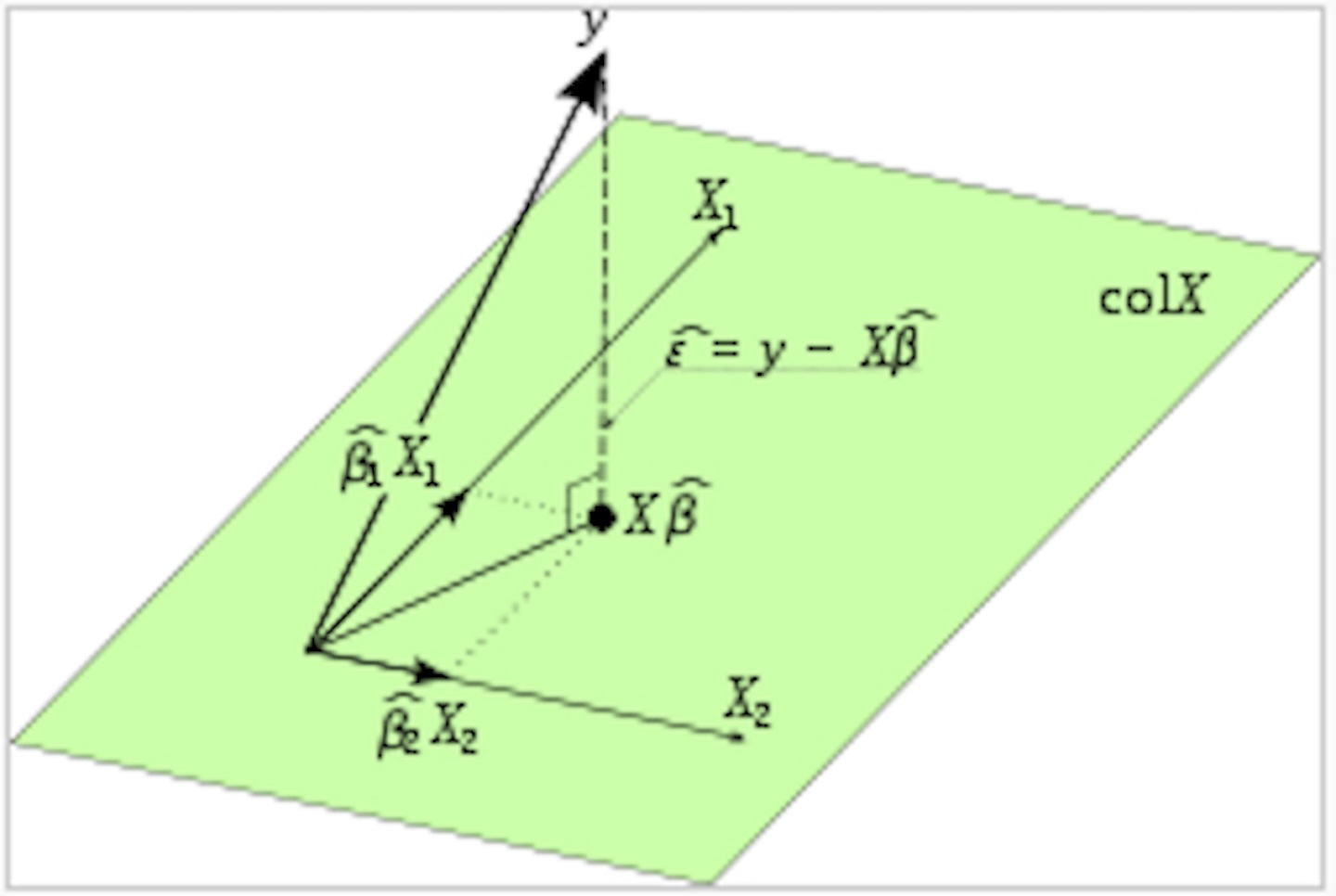
Non-Full Rank Case

Model: \(\mathbf{Y}= \boldsymbol{\mu}+ \boldsymbol{\epsilon}\)
Assumption: \(\boldsymbol{\mu}\in C(\mathbf{X})\) for \(\mathbf{X}\in \mathbb{R}^{n \times p}\)
What if the rank of \(\mathbf{X}\), \(r(\mathbf{X}) \equiv r \ne p\)?
Still have result that the OLS/MLE solution satisfies \[\mathbf{P}_\mathbf{X}\mathbf{Y}= \mathbf{X}\hat{\boldsymbol{\beta}}\]
How can we characterize \(\mathbf{P}\) and \(\hat{\boldsymbol{\beta}}\) in this case? 2 cases

\(p \le n\), \(r(\mathbf{X}) \ne p\) \(\Rightarrow r(\mathbf{X}) < p\)
\(p \gt n\), \(r(\mathbf{X}) \ne p\)

Focus on the first case for OLS/MLE for now…

Model Space

\(\boldsymbol{{\cal M}}= C(\mathbf{X})\) is an \(r\)-dimensional subspace of \(\mathbb{R}^n\)
\(\boldsymbol{{\cal M}}\) has an \((n - r)\)-dimensional orthogonal complement \(\boldsymbol{{\cal N}}\)
each \(\mathbf{y}\in \mathbb{R}^n\) has a unique representation as \[ \mathbf{y}= \hat{\mathbf{y}}+ \mathbf{e}\] for \(\hat{\mathbf{y}}\in \boldsymbol{{\cal M}}\) and \(\mathbf{e}\in \boldsymbol{{\cal N}}\)
\(\hat{\mathbf{y}}\) is the orthogonal projection of \(\mathbf{y}\) onto \(\boldsymbol{{\cal M}}\) and is the OLS/MLE estimate of \(\boldsymbol{\mu}\) that satisfies \[\mathbf{P}_\mathbf{X}\mathbf{y}= \mathbf{X}\hat{\boldsymbol{\beta}}= \hat{\mathbf{y}}\]
\(\mathbf{X}^T\mathbf{X}\) is not invertible so need another way to represent \(\mathbf{P}_\mathbf{X}\) and \(\hat{\boldsymbol{\beta}}\)

Spectral Decomposition (SD)

Every symmetric \(n \times n\) matrix, \({\mathbf{S}}\), has an eigen decomposition \({\mathbf{S}}= \mathbf{U}\boldsymbol{\Lambda}\mathbf{U}^T\)

\(\boldsymbol{\Lambda}\) is a diagonal matrix with eigenvalues \((\lambda_1, \ldots, \lambda_n)\) of \({\mathbf{S}}\)
\(\mathbf{U}\) is a \(n \times n\) orthogonal matrix \(\mathbf{U}^T\mathbf{U}= \mathbf{U}\mathbf{U}^T = \mathbf{I}_n\) ( \(\mathbf{U}^{-1} = \mathbf{U}^T\))
the columns of \(\mathbf{U}\) from an Orthonormal Basis (ONB) for \(\mathbb{R}^n\)
the columns of \(\mathbf{U}\) associated with non-zero eigenvalues form an ONB for \(C({\mathbf{S}})\)
the number of non-zero eigenvalues is the rank of \({\mathbf{S}}\)
the columns of \(\mathbf{U}\) associated with zero eigenvalues form an ONB for \(C({\mathbf{S}})^\perp\)
\({\mathbf{S}}^d = \mathbf{U}\boldsymbol{\Lambda}^d \mathbf{U}^T\) (matrix powers)

Positive Definite and Non-Negative Definite Matrices

Definition: B.21 Positive Definite and Non-Negative Definite

A symmetric matrix \({\mathbf{S}}\) is positive definite (\({\mathbf{S}}\gt 0\)) if and only if \(\mathbf{x}^T{\mathbf{S}}\mathbf{x}> 0\) for \(\mathbf{x}\in \mathbb{R}^n\), \(\mathbf{x}\ne \mathbf{0}_n\), and positive semi-definite or non-negative definite (\({\mathbf{S}}\ge 0\)) if and only if \(\mathbf{x}^T{\mathbf{S}}\mathbf{x}\ge 0\) for \(\mathbf{x}\in \mathbb{R}^n\), \(\mathbf{x}\ne \mathbf{0}_n\)

Exercise

Show that a symmetric matrix \({\mathbf{S}}\) is positive definite if and only if its eigenvalues are all strictly greater than zero, and positive semi-definite if all the eigenvalues are non-negative.

Projections

Let \(\mathbf{P}\) be an orthogonal projection matrix onto \(\boldsymbol{{\cal M}}\), then

the eigenvalues of \(\mathbf{P}\), \(\lambda_i\), are either zero or one
the trace of \(\mathbf{P}\) is the rank of \(\mathbf{P}\)
the dimension of the subspace that \(\mathbf{P}\) projects onto is the rank of \(\mathbf{P}\)
the columns of \(\mathbf{U}_r = [u_1, u_2, \ldots u_r]\) form an ONB for the \(C(\mathbf{P})\)
the projection \(\mathbf{P}\) has the representation \(\mathbf{P}= \mathbf{U}_r \mathbf{U}_r^T = \sum_{i = 1}^r u_i u_i^T\) (the sum of \(r\) rank \(1\) projections)
the projection \(\mathbf{I}_n - \mathbf{P}= \mathbf{I}- \mathbf{U}_r \mathbf{U}_r^T = \mathbf{U}_\perp \mathbf{U}_\perp^T\) where \(\mathbf{U}_\perp = [u_{r+1}, \ldots u_n]\) is an orthogonal projection onto \(\boldsymbol{{\cal N}}\)

MLE/OLS:

\(\mathbf{P}_X \mathbf{y}= \mathbf{U}_r \mathbf{U}_r^T \mathbf{y}= \mathbf{U}_r \tilde{\boldsymbol{\beta}}\)
Claim \(\tilde{\boldsymbol{\beta}}\) is a MLE/OLS estimate of \(\boldsymbol{\beta}\) where \(\tilde{\mathbf{X}}= \mathbf{U}_r\).

Singular Value Decomposition & Connections to Spectral Decompositions

A matrix \(\mathbf{X}\in \mathbb{R}^{n \times p}\), \(p \le n\) has a singular value decomposition \[\mathbf{X}= \mathbf{U}_p \mathbf{D}\mathbf{V}^T\]

\(\mathbf{U}_p\) is a \(n \times p\) matrix with the first \(p\) eigenvectors in \(\mathbf{U}\) associated with the \(p\) largest eigenvectors of \(\mathbf{X}\mathbf{X}^T = \mathbf{U}\boldsymbol{\Lambda}\mathbf{U}^T\) with \(\mathbf{U}_p^T\mathbf{U}_p = I_p\) but \(\mathbf{U}_p \mathbf{U}_p^T \ne \mathbf{I}_n\) (or \(\mathbf{P}_p\))
\(\mathbf{V}\) is a \(p \times p\) orthogonal matrix associated with the \(p\) eigenvectors of \(\mathbf{X}^T\mathbf{X}= \mathbf{V}\boldsymbol{\Lambda}_p \mathbf{V}^T\) where \(\boldsymbol{\Lambda}_p\) is the diagonal matrix of eigenvalues associated with the \(p\) largest eigenvalues of \(\boldsymbol{\Lambda}\)
\(\mathbf{D}\) = \(\boldsymbol{\Lambda}_p^{1/2}\) are the singular values
if \(\mathbf{X}\) has rank \(r < p\), then \(C(\mathbf{X}) = C(\mathbf{U}_p) = C(\mathbf{U}_r)\), where \(\mathbf{U}_r\) are the eigenvectors of \(\mathbf{U}\) or \(\mathbf{U}_p\) associated with the non-zero eigenvalues.
\(\mathbf{U}_r\) is an ONB for \(C(X)\)

MLE/OLS for non-full rank case

if \(\mathbf{X}^T\mathbf{X}\) is invertible, \(\mathbf{P}_X = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T\) and \(\hat{\boldsymbol{\beta}}\) is the unique estimator that satisfies \(\mathbf{P}_\mathbf{X}\mathbf{y}= \mathbf{X}\hat{\boldsymbol{\beta}}\) or \(\hat{\boldsymbol{\beta}}= (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T\mathbf{y}\)
if \(\mathbf{X}^T\mathbf{X}\) is not invertible, replace \(\mathbf{X}\) by \(\tilde{\mathbf{X}}\) that is rank \(r\)
or represent \(\mathbf{P}_\mathbf{X}= \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-} \mathbf{X}^T\) where \((\mathbf{X}^T\mathbf{X})^{-}\) is a generalized inverse of \(\mathbf{X}^T\mathbf{X}\) and \(\hat{\boldsymbol{\beta}}= (\mathbf{X}^T\mathbf{X})^{-}\mathbf{X}^T \mathbf{y}\)

Generalized Inverses

Definition: Generalized-Inverse (B.36)

A generalized inverse of any matrix \(\mathbf{A}\): \(\mathbf{A}^{-}\) satisfies \(\mathbf{A}\mathbf{A}^- \mathbf{A}= \mathbf{A}\)

A generalized inverse of \(\mathbf{A}\) symmetric always exists!

Theorem: Christensen B.39

If \(\mathbf{G}_1\) and \(\mathbf{G}_2\) are generalized inverses of \(\mathbf{A}\) then \(\mathbf{G}_1 \mathbf{A}\mathbf{G}_2\) is also a generalized inverse of \(\mathbf{A}\)

if \(\mathbf{A}\) is symmetric, then \(\mathbf{A}^-\) need not be!

Orthogonal Projections in General

Lemma B.43

If \(\mathbf{G}\) and \(\mathbf{H}\) are generalized inverses of \(\mathbf{X}^T\mathbf{X}\) then \[\begin{align*} \mathbf{X}\mathbf{G}\mathbf{X}^T \mathbf{X}& = \mathbf{X}\mathbf{H}\mathbf{X}^T \mathbf{X}= \mathbf{X}\\ \mathbf{X}\mathbf{G}\mathbf{X}^T & = \mathbf{X}\mathbf{H}\mathbf{X}^T \end{align*}\]

Theorem: B.44

\(\mathbf{X}(\mathbf{X}^T\mathbf{X})^-\mathbf{X}^T\) is an orthogonal projection onto \(C(\mathbf{X})\).

We need to show that (i) \(\mathbf{P}\mathbf{m}= \mathbf{m}\) for \(\mathbf{m}\in C(\mathbf{X})\) and (ii) \(\mathbf{P}\mathbf{n}= 0\) for \(\mathbf{n}\in C(\mathbf{X})^\perp\).

For \(\mathbf{m}\in C(\mathbf{X})\), write \(\mathbf{m}= \mathbf{X}\mathbf{b}\). Then \(\mathbf{P}\mathbf{m}= \mathbf{P}\mathbf{X}\mathbf{b}= \mathbf{X}(\mathbf{X}^T\mathbf{X})^-\mathbf{X}^T \mathbf{X}\mathbf{b}\) and by Lemma B43, we have that \(\mathbf{X}(\mathbf{X}^T\mathbf{X})^-\mathbf{X}^T \mathbf{X}\mathbf{b}= \mathbf{X}\mathbf{b}= \mathbf{m}\)
For \(\mathbf{n}\perp C(\mathbf{X})\), \(\mathbf{P}\mathbf{n}= \mathbf{X}(\mathbf{X}^T\mathbf{X})^-\mathbf{X}^T \mathbf{n}= \mathbf{0}_n\) as \(C(\mathbf{X})^\perp = N(\mathbf{X}^T)\).

MLEs & OLS

MLE/OLS satisfies

\(\mathbf{P}\mathbf{y}= \mathbf{X}\hat{\boldsymbol{\beta}}\)
\(\mathbf{P}\mathbf{y}= \mathbf{X}(\mathbf{X}^T\mathbf{X})^-\mathbf{X}^T \mathbf{X}\hat{\boldsymbol{\beta}}= \mathbf{X}\hat{\boldsymbol{\beta}}\) (does not depend on choice of generalized inverse)
\(\hat{\boldsymbol{\beta}}= (\mathbf{X}^T\mathbf{X})^-\mathbf{X}^T \mathbf{y}\)
\(\hat{\boldsymbol{\beta}}\) is not unique - does depend on choice of generalized inverse unless \(\mathbf{X}\) is full rank

Moore-Penrose Generalized Inverse:

Decompose symmetric \(\mathbf{A}= \mathbf{U}\boldsymbol{\Lambda}\mathbf{U}^T\) (i.e \(\mathbf{X}^T\mathbf{X}\))
\(\mathbf{A}^-_{MP} = \mathbf{U}\boldsymbol{\Lambda}^- \mathbf{U}^T\)
\(\boldsymbol{\Lambda}^-\) is diagonal with \[ \lambda_i^- = \left\{ \begin{array}{l} 1/\lambda_i \text{ if } \lambda_i \neq 0 \\ 0 \quad \, \text{ if } \lambda_i = 0 \end{array} \right.\]
Symmetric \(\mathbf{A}^-_{MP} = (\mathbf{A}^-_{MP})^T\)
Reflexive \(\mathbf{A}^-_{MP}\mathbf{A}\mathbf{A}^-_{MP} = \mathbf{A}^-_{MP}\)

Show that \(\mathbf{A}_{MP}^-\) is a generalized inverse of \(\mathbf{A}\)
Can you construct another generalized inverse of \(\mathbf{X}^T\mathbf{X}\) ?
Can you find the Moore-Penrose generalized inverse of \(\mathbf{X}\in \mathbb{R}^{n \times p}\)?

Properties of OLS (full rank case)

How good is \(\hat{\boldsymbol{\beta}}\) as an estimator of \(\beta\)

\(\hat{\boldsymbol{\beta}}= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T \mathbf{Y}= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T \mathbf{X}\boldsymbol{\beta}+ (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\boldsymbol{\epsilon}= \boldsymbol{\beta}+ (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\boldsymbol{\epsilon}\)
don’t know \(\boldsymbol{\epsilon}\), but can talk about behavior on average over
- different runs of an experiment
- different samples from a population
- different values of \(\boldsymbol{\epsilon}\)
with minimal assumption \(\textsf{E}[\boldsymbol{\epsilon}] = \mathbf{0}_n\), \[\begin{align*} \textsf{E}[\hat{\boldsymbol{\beta}}] & = \textsf{E}[(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}\boldsymbol{\beta}+ (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\boldsymbol{\epsilon}]\\ & = \boldsymbol{\beta}+ (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\textsf{E}[\boldsymbol{\epsilon}] \\ & = \boldsymbol{\beta} \end{align*}\]
Bias of \(\hat{\boldsymbol{\beta}}\), \(\text{Bias}[\hat{\boldsymbol{\beta}}] = \textsf{E}[\hat{\boldsymbol{\beta}}- \boldsymbol{\beta}] = \mathbf{0}_p\)
\(\hat{\boldsymbol{\beta}}\) is an unbiased estimator of \(\boldsymbol{\beta}\) if \(\boldsymbol{\mu}\in C(\mathbf{X})\)

Class of Unbiased Estimators

Class of linear statistical models: \[\begin{align*} \mathbf{Y}& = \mathbf{X}\boldsymbol{\beta}+ \boldsymbol{\epsilon}\\ \boldsymbol{\epsilon}& \sim P \\ P & \in \cal{P} \end{align*}\]

An estimator \(\tilde{\boldsymbol{\beta}}\) is unbiased for \(\boldsymbol{\beta}\) if \(\textsf{E}_P[\tilde{\boldsymbol{\beta}}] = \boldsymbol{\beta}\quad \forall \boldsymbol{\beta}\in \mathbb{R}^p\) and \(P \in \cal{P}\)

Examples:

\(\cal{P}_1= \{P = \textsf{N}(\mathbf{0}_n ,\mathbf{I}_n)\}\)

\(\cal{P}_2 = \{P = \textsf{N}(\mathbf{0}_n ,\sigma^2 \mathbf{I}_n), \sigma^2 >0\}\)

\(\cal{P}_3 = \{P = \textsf{N}(\mathbf{0}_n ,\boldsymbol{\Sigma}), \boldsymbol{\Sigma}\in \cal{{\cal{S}}}^+ \}\) (\(\cal{{\cal{S}}}^+\) is the set of all \(n \times n\) symmetric positive definite matrices.)

\(\cal{P}_4\) is the set of distributions with \(\textsf{E}_P[\boldsymbol{\epsilon}] = \mathbf{0}_n\) and \(\textsf{E}_P[\boldsymbol{\epsilon}\boldsymbol{\epsilon}^T] \gt 0\)

\(\cal{P}_5\) is the set of distributions with \(\textsf{E}_P[\boldsymbol{\epsilon}] = \mathbf{0}_n\) and \(\textsf{E}_P[\boldsymbol{\epsilon}\boldsymbol{\epsilon}^T] \ge 0\)

Linear Unbiased Estimation

Exercise

Explain why an estimator that is unbiased for the model with parameter space \(\boldsymbol{\beta}\in \mathbb{R}^p\) and \(P \in \cal{P}_{k+1}\) is unbiased for the model with parameter space \(\boldsymbol{\beta}\in \mathbb{R}^p\) and \(P \in \cal{P}_{k}\) .
Find an estimator that is unbiased for \(\boldsymbol{\beta}\in \mathbb{R}^p\) and \(P \in \cal{P}_{1}\) that but is biased for \(\boldsymbol{\beta}\in \mathbb{R}^p\) and \(P \in \cal{P}_{2}\).

Restrict attention to linear unbiased estimators

Definition: Linear Unbiased Estimators (LUEs)

An estimator \(\tilde{\boldsymbol{\beta}}\) is a Linear Unbiased Estimator (LUE) of \(\boldsymbol{\beta}\) if

linearity: \(\tilde{\boldsymbol{\beta}}= \mathbf{A}\mathbf{Y}\) for \(\mathbf{A}\in \mathbb{R}^{p \times n}\)
unbiasedness: \(\textsf{E}[\tilde{\boldsymbol{\beta}}] = \boldsymbol{\beta}\) for all \(\boldsymbol{\beta}\in \mathbb{R}^p\)

Are there other LUEs besides the OLS/MLE estimator?
Which is “best”? (and in what sense?)