Bayesian Model Averaging and Variable Selection

STA721: Lecture 18

Merlise Clyde

Duke University

US Air Example

library(BAS)
data(usair, package="HH")
poll.bma = bas.lm(log(SO2) ~ temp + log(mfgfirms) +
                             log(popn) + wind +
                             precip + raindays,
                  data=usair,
                  prior="JZS",  #Jeffrey-Zellner-Siow
                  alpha=nrow(usair), # n
                  n.models=2^6,
                  modelprior = uniform(),
                  method="deterministic")

Summary

summary(poll.bma, n.models=4)
              P(B != 0 | Y) model 1   model 2   model 3   model 4
Intercept        1.00000000 1.00000 1.0000000 1.0000000 1.0000000
temp             0.91158530 1.00000 1.0000000 1.0000000 1.0000000
log(mfgfirms)    0.31718916 0.00000 0.0000000 0.0000000 1.0000000
log(popn)        0.09223957 0.00000 0.0000000 0.0000000 0.0000000
wind             0.29394451 0.00000 0.0000000 0.0000000 1.0000000
precip           0.28384942 0.00000 1.0000000 0.0000000 1.0000000
raindays         0.22903262 0.00000 0.0000000 1.0000000 0.0000000
BF                       NA 1.00000 0.3286643 0.2697945 0.2655873
PostProbs                NA 0.29410 0.0967000 0.0794000 0.0781000
R2                       NA 0.29860 0.3775000 0.3714000 0.5427000
dim                      NA 2.00000 3.0000000 3.0000000 5.0000000
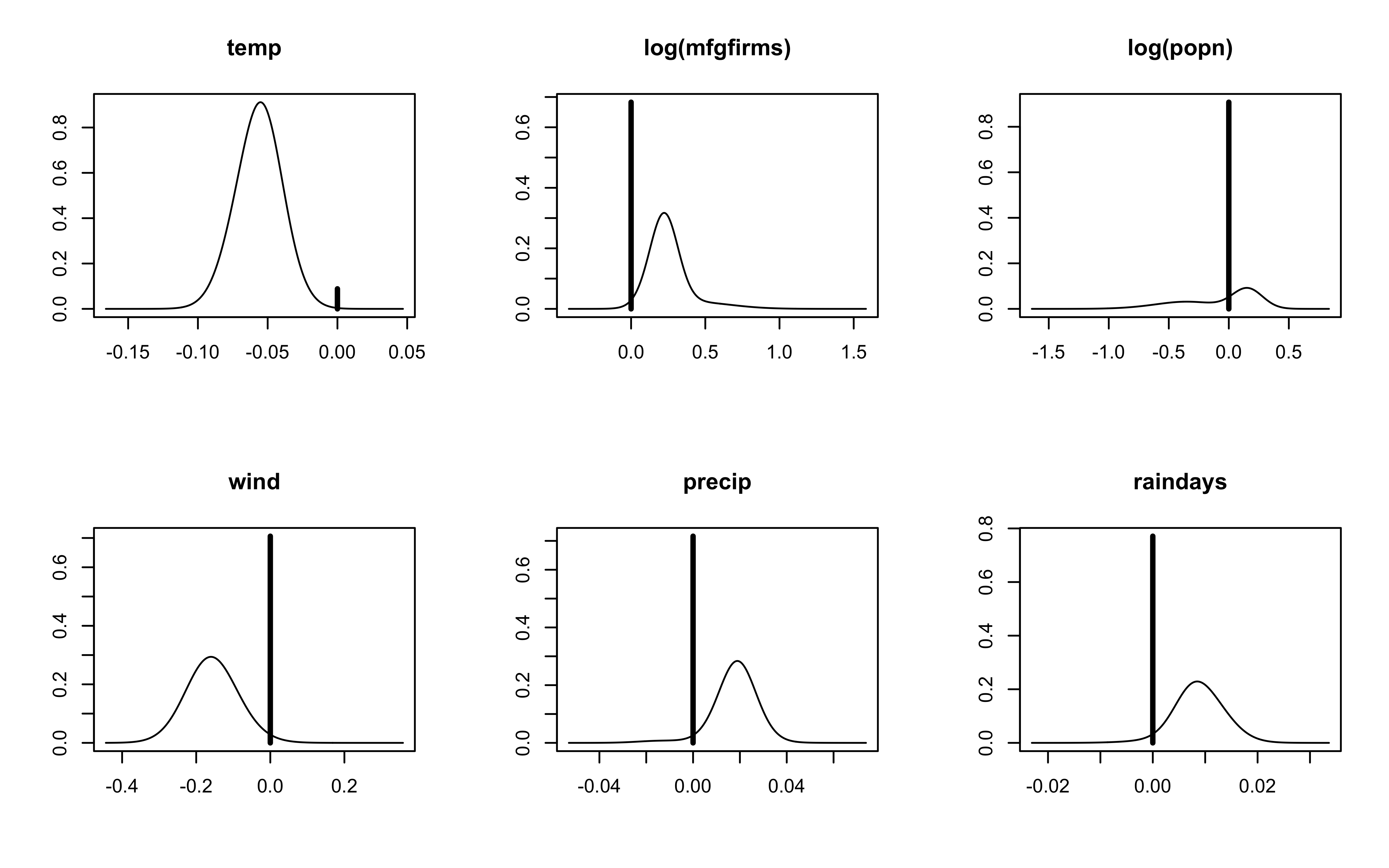
logmarg                  NA 3.14406 2.0313422 1.8339656 1.8182487

Plots of Coefficients

 beta = coef(poll.bma)
 par(mfrow=c(2,3));  plot(beta, subset=2:7,ask=F)

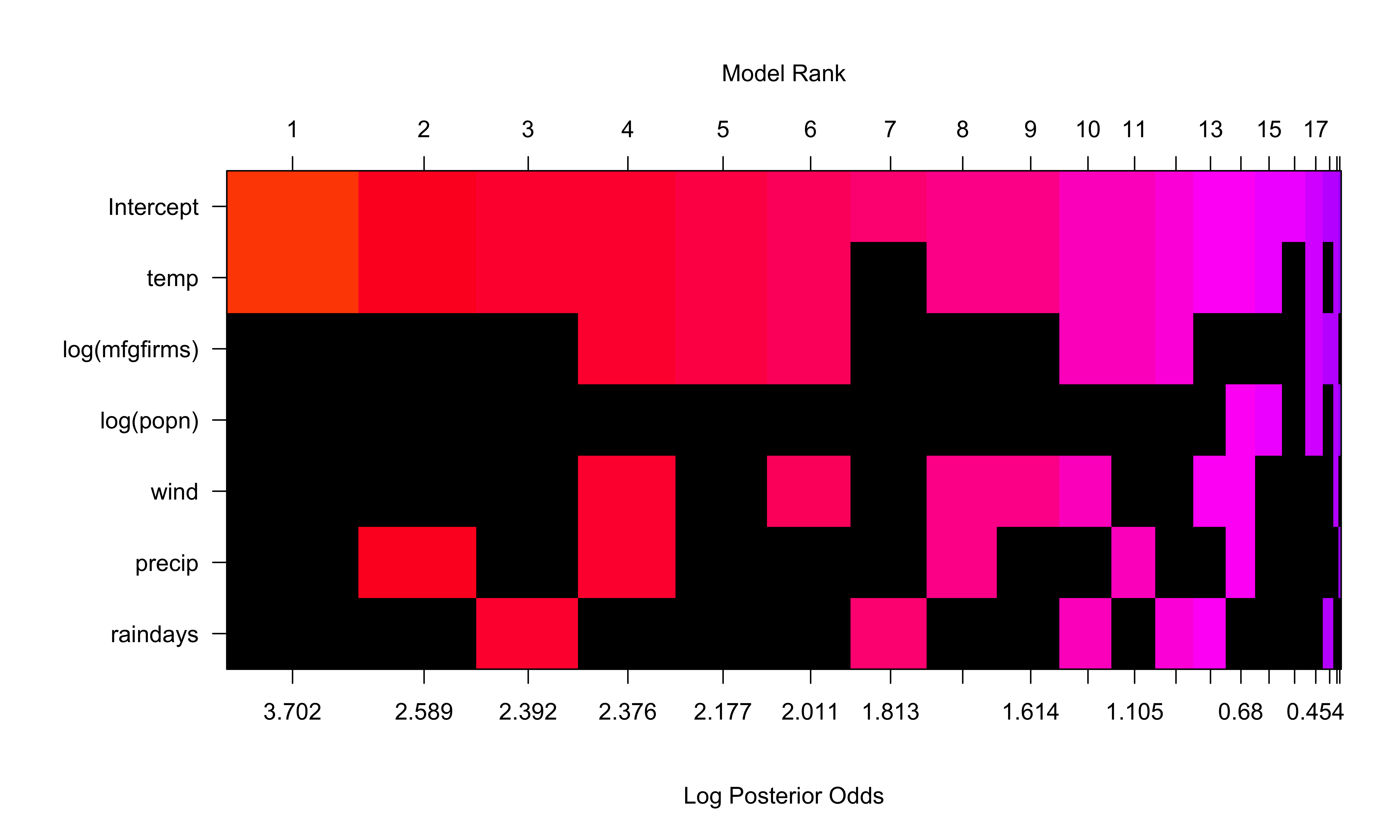
Posterior Distribution with Uniform Prior on Model Space

image(poll.bma, rotate=FALSE)

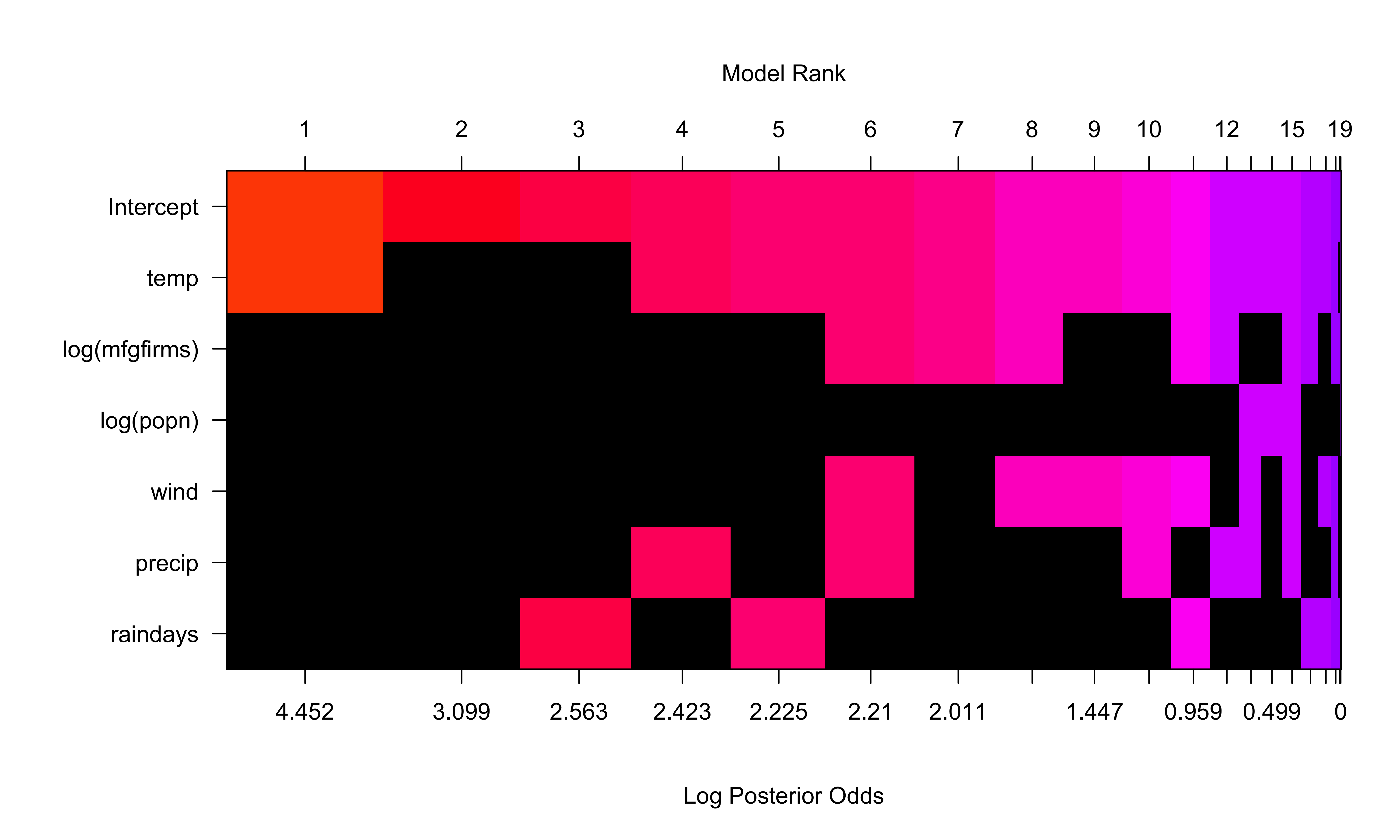
Posterior Distribution with BB(1,1) Prior on Model Space

poll.bb.bma = bas.lm(log(SO2) ~ temp + log(mfgfirms) +
                                log(popn) + wind +
                                precip + raindays,
                     data=usair,
                     prior="JZS",
                     alpha=nrow(usair),
                     n.models=2^6,  #enumerate
                     modelprior=beta.binomial(1,1))

Posterior Distribution with BB(1,1) Prior on Model Space

image(poll.bb.bma, rotate=FALSE)

Diabetes Example

set.seed(8675309)
source("yX.diabetes.train.txt")
diabetes.train = as.data.frame(diabetes.train)
source("yX.diabetes.test.txt")
diabetes.test = as.data.frame(diabetes.test)
colnames(diabetes.test)[1] = "y"

str(diabetes.train)
'data.frame':   342 obs. of  65 variables:
 $ y      : num  -0.0147 -1.0005 -0.1444 0.6987 -0.2222 ...
 $ age    : num  0.7996 -0.0395 1.7913 -1.8703 0.113 ...
 $ sex    : num  1.064 -0.937 1.064 -0.937 -0.937 ...
 $ bmi    : num  1.296 -1.081 0.933 -0.243 -0.764 ...
 $ map    : num  0.459 -0.553 -0.119 -0.77 0.459 ...
 $ tc     : num  -0.9287 -0.1774 -0.9576 0.256 0.0826 ...
 $ ldl    : num  -0.731 -0.402 -0.718 0.525 0.328 ...
 $ hdl    : num  -0.911 1.563 -0.679 -0.757 0.171 ...
 $ tch    : num  -0.0544 -0.8294 -0.0544 0.7205 -0.0544 ...
 $ ltg    : num  0.4181 -1.4349 0.0601 0.4765 -0.6718 ...
 $ glu    : num  -0.371 -1.936 -0.545 -0.197 -0.979 ...
 $ age^2  : num  -0.312 -0.867 1.925 2.176 -0.857 ...
 $ bmi^2  : num  0.4726 0.1185 -0.0877 -0.6514 -0.2873 ...
 $ map^2  : num  -0.652 -0.573 -0.815 -0.336 -0.652 ...
 $ tc^2   : num  -0.091 -0.6497 -0.0543 -0.6268 -0.6663 ...
 $ ldl^2  : num  -0.289 -0.521 -0.3 -0.45 -0.555 ...
 $ hdl^2  : num  -0.0973 0.8408 -0.3121 -0.2474 -0.5639 ...
 $ tch^2  : num  -0.639 -0.199 -0.639 -0.308 -0.639 ...
 $ ltg^2  : num  -0.605 0.78 -0.731 -0.567 -0.402 ...
 $ glu^2  : num  -0.578 1.8485 -0.4711 -0.6443 -0.0258 ...
 $ age:sex: num  0.69 -0.139 1.765 1.609 -0.284 ...
 $ age:bmi: num  0.852 -0.142 1.489 0.271 -0.271 ...
 $ age:map: num  0.0349 -0.3346 -0.5862 1.1821 -0.3025 ...
 $ age:tc : num  -0.978 -0.246 -1.927 -0.72 -0.244 ...
 $ age:ldl: num  -0.803 -0.203 -1.504 -1.2 -0.182 ...
 $ age:hdl: num  -0.7247 0.0147 -1.2661 1.6523 0.1046 ...
 $ age:tch: num  -0.254 -0.176 -0.31 -1.598 -0.216 ...
 $ age:ltg: num  0.0644 -0.2142 -0.163 -1.1657 -0.3474 ...
 $ age:glu: num  -0.636 -0.239 -1.359 0.071 -0.438 ...
 $ sex:bmi: num  1.304 0.935 0.915 0.142 0.635 ...
 $ sex:map: num  0.258 0.289 -0.381 0.5 -0.697 ...
 $ sex:tc : num  -1.02 0.131 -1.051 -0.274 -0.112 ...
 $ sex:ldl: num  -0.927 0.236 -0.913 -0.638 -0.452 ...
 $ sex:hdl: num  -0.647 -1.188 -0.377 1.189 0.238 ...
 $ sex:tch: num  -0.411 0.47 -0.411 -1.062 -0.296 ...
 $ sex:ltg: num  0.2988 1.2093 -0.0866 -0.6032 0.4857 ...
 $ sex:glu: num  -0.6171 1.6477 -0.8069 -0.0239 0.7283 ...
 $ bmi:map: num  0.189 0.191 -0.477 -0.195 -0.702 ...
 $ bmi:tc : num  -1.5061 -0.0595 -1.1853 -0.3231 -0.3239 ...
 $ bmi:ldl: num  -1.267 0.183 -0.976 -0.407 -0.536 ...
 $ bmi:hdl: num  -0.869 -1.41 -0.286 0.586 0.251 ...
 $ bmi:tch: num  -0.505 0.505 -0.484 -0.614 -0.388 ...
 $ bmi:ltg: num  0.1014 1.1613 -0.4085 -0.5893 0.0716 ...
 $ bmi:glu: num  -0.862 1.693 -0.89 -0.337 0.358 ...
 $ map:tc : num  -0.687 -0.148 -0.131 -0.451 -0.21 ...
 $ map:ldl: num  -0.5407 0.0388 -0.1034 -0.6114 -0.036 ...
 $ map:hdl: num  -0.235 -0.672 0.254 0.745 0.252 ...
 $ map:tch: num  -0.29 0.207 -0.258 -0.835 -0.29 ...
 $ map:ltg: num  -0.214 0.428 -0.427 -0.811 -0.748 ...
 $ map:glu: num  -0.541 0.659 -0.314 -0.23 -0.812 ...
 $ tc:ldl : num  -0.144 -0.551 -0.139 -0.509 -0.581 ...
 $ tc:hdl : num  0.8363 -0.3457 0.6304 -0.2579 -0.0392 ...
 $ tc:tch : num  -0.405 -0.326 -0.404 -0.295 -0.451 ...
 $ tc:ltg : num  -0.901 -0.259 -0.571 -0.392 -0.569 ...
 $ tc:glu : num  0.0202 0.0196 0.2073 -0.396 -0.4283 ...
 $ ldl:hdl: num  0.889 -0.446 0.705 -0.207 0.26 ...
 $ ldl:tch: num  -0.463 -0.243 -0.463 -0.21 -0.506 ...
 $ ldl:ltg: num  -0.6536 0.2724 -0.3783 -0.0708 -0.5638 ...
 $ ldl:glu: num  -0.0194 0.4995 0.1032 -0.4013 -0.6234 ...
 $ hdl:tch: num  0.703 -0.5 0.692 0.171 0.651 ...
 $ hdl:ltg: num  0.0179 -1.9846 0.3839 0.0399 0.3043 ...
 $ hdl:glu: num  0.654 -2.948 0.689 0.452 0.113 ...
 $ tch:ltg: num  -0.592 0.531 -0.574 -0.253 -0.537 ...
 $ tch:glu: num  -0.371 1.114 -0.362 -0.522 -0.34 ...
 $ ltg:glu: num  -0.584 2.184 -0.468 -0.526 0.183 ...

MCMC with BAS

library(BAS)
diabetes.bas = bas.lm(y ~ ., data=diabetes.train,
                      prior = "JZS",
                      method="MCMC",
                      n.models = 10000,
                      MCMC.iterations=500000,
                      thin = 10,
                      initprobs="eplogp",
                      force.heredity=FALSE)
   user  system elapsed 
 10.538   0.574  11.113 
[1] "number of unique models 5905"

  • increase MCMC.iterations?

  • check diagnostics

Estimates of Posterior Probabilities

  • relative frequencies \(\hat{P}_{RF}(\boldsymbol{\gamma}\mid \mathbf{Y}) = \frac{\text{# times } \boldsymbol{\gamma}\in S }{S}\)

    • ergodic average converges to \(p(\boldsymbol{\gamma}\mid \mathbf{Y})\) as \(S \to \infty\)

    • asymptoptically unbaised

  • renormalized posterior probabilities \(\hat{P}_{RN}(\boldsymbol{\gamma}\mid \mathbf{Y}) = \frac{p(\mathbf{Y}\mid \boldsymbol{\gamma}) p(\boldsymbol{\gamma})} {\sum_{\boldsymbol{\gamma}\in S} p(\mathbf{Y}\mid \boldsymbol{\gamma}) p(\boldsymbol{\gamma})}\)

    • also asymptoptically unbaised

    • Fisher consistent (e.g if we happen to enumerate all models in \(S\) iterations we recover the truth)

  • if we run long enough the two should agree

  • also look at other summaries i.e posterior inclusion probabilities \[\hat{p}(\gamma_j = 1 \mid \mathbf{Y}) = \sum_S \gamma_j \hat{P}(\boldsymbol{\gamma}\mid \mathbf{Y})\]

Diagnostic Plot

diagnostics(diabetes.bas, type="pip")
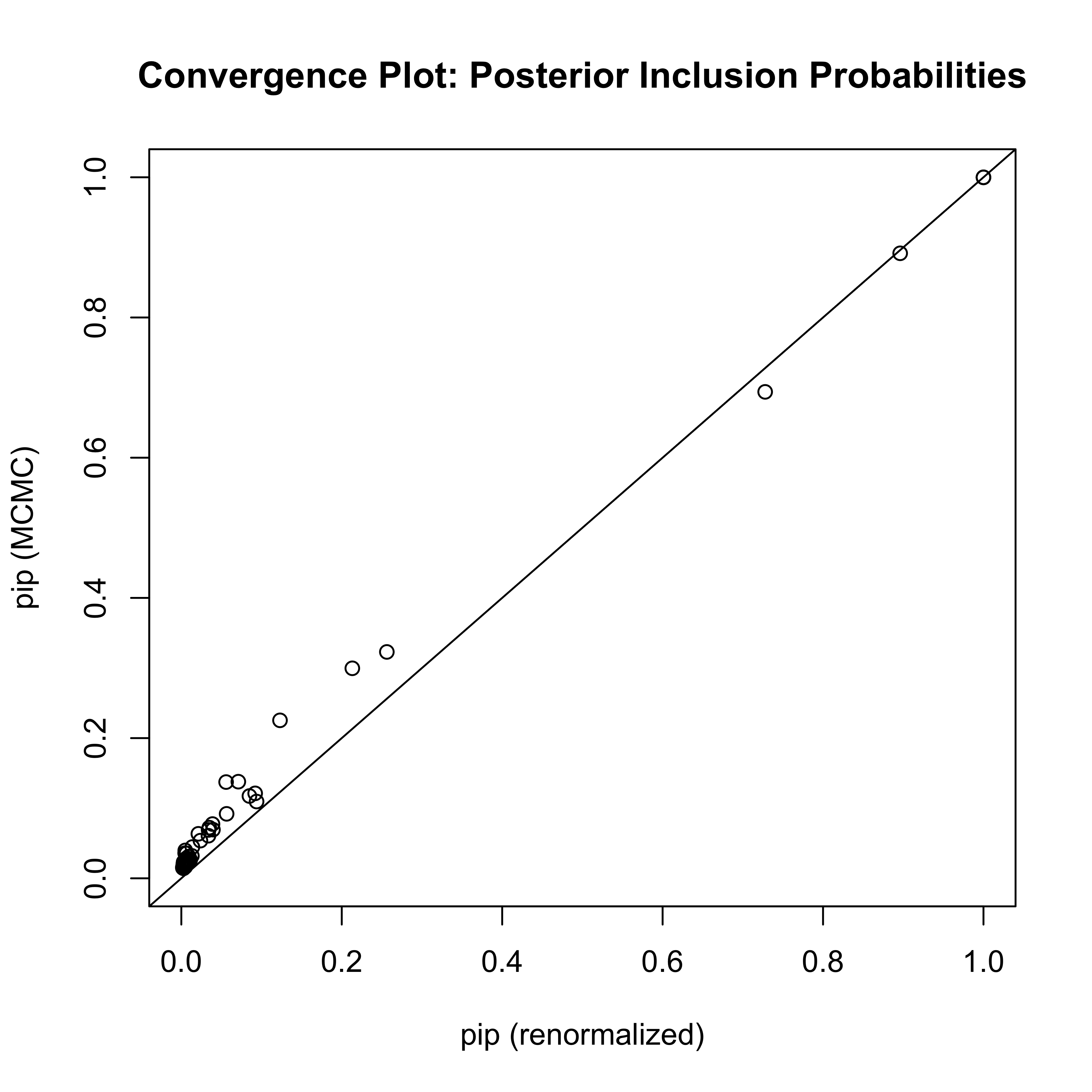
  • model probabilities converge much slower!

Out of Sample Prediction

  • What is the optimal value to predict \(\mathbf{Y}^{\text{test}}\) given \(\mathbf{Y}\) under squared error?

  • Iterated expectations leads to BMA for \(\textsf{E}[\mathbf{Y}^{\text{test}} \mid \mathbf{Y}]\)

  • Prediction under model averaging \[\hat{Y} = \sum_S (\hat{\alpha}_\boldsymbol{\gamma}+ \mathbf{X}_{\boldsymbol{\gamma}}^{\text{test}} \hat{\boldsymbol{\beta}}_{\boldsymbol{\gamma}}) \hat{p}(\boldsymbol{\gamma}\mid \mathbf{Y})\]

pred.bas = predict(diabetes.bas,
                   newdata=diabetes.test,
                   estimator="BMA",
                   se=TRUE)
mean((pred.bas$fit- diabetes.test$y)^2)
[1] 0.4556414

Credible Intervals & Coverage

  • posterior predictive distribution \[ p(\mathbf{y}^{\text{test}} \mid \mathbf{y}) = \sum_\boldsymbol{\gamma}p(\mathbf{y}^{\text{test}} \mid \mathbf{y}, \boldsymbol{\gamma})p(\boldsymbol{\gamma}\mid \mathbf{y}) \]

  • integrate out \(\alpha\) and \(\boldsymbol{\beta_\gamma}\) to get a normal predictive given \(\phi\) and \(\boldsymbol{\gamma}\) (and \(\mathbf{y}\))

  • integrate out \(\phi\) to get a t distribution given \(\boldsymbol{\gamma}\) and \(\mathbf{y}\)

  • credible intervals via sampling

    • sample a model from \(p(\boldsymbol{\gamma}\mid \mathbf{y})\)
    • conditional on a model sample \(y \sim p(\mathbf{y}^{\text{test}} \mid \mathbf{y}, \boldsymbol{\gamma})\)
    • compute quantiles from sample \(y\)
ci.bas = confint(pred.bas);
coverage = mean(diabetes.test$y > ci.bas[,1] & diabetes.test$y < ci.bas[,2])
coverage
[1] 1

95% Prediction intervals

plot(ci.bas)
NULL
points(diabetes.test$y, col=2, pch=15)

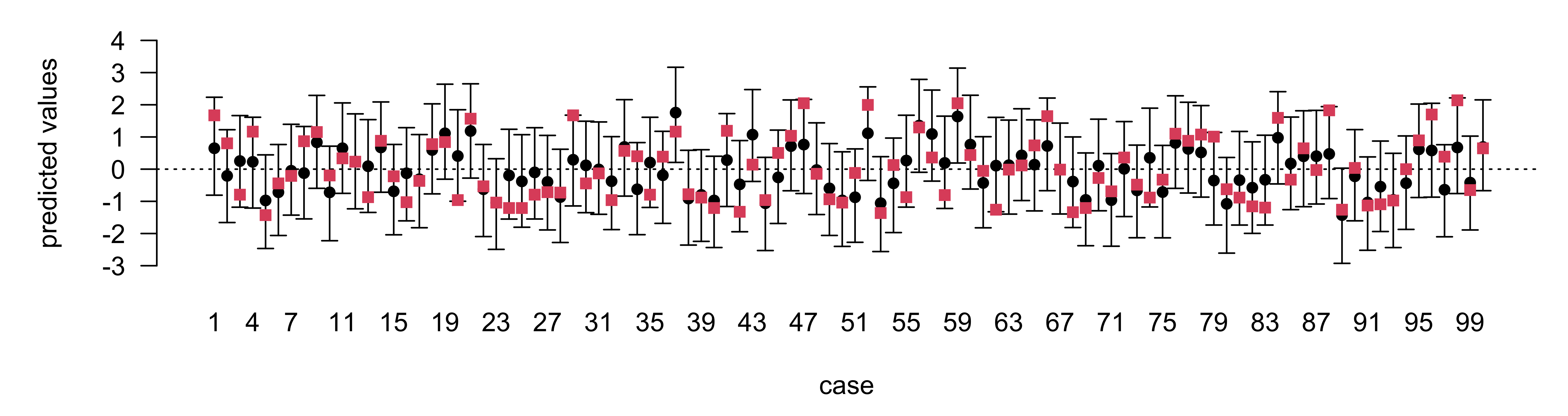
Selection and Prediction

  • BMA - optimal for squared error loss Bayes \[\textsf{E}[\| \mathbf{Y}^{\text{test}} - a\|^2 \mid \mathbf{y}] = \textsf{E}[\| \mathbf{Y}^{\text{test}} - \textsf{E}[\mathbf{Y}^{\text{test}}\mid \mathbf{y}] \|^2 \mid \mathbf{y}] + \| \textsf{E}[\mathbf{Y}^{\text{test}}\mid \mathbf{y}] - a\|^2 \]

  • What if we want to use only a single model for prediction under squared error loss?

  • HPM: Highest Posterior Probability model is optimal for selection, but not prediction

  • MPM: Median Probability model (select model where PIP > 0.5) (optimal under certain conditions; nested models)

  • BPM: Best Probability Model - Model closest to BMA under loss (usually includes more predictors than HPM or MPM)

Example

pred.bas = predict(diabetes.bas,
                   newdata=diabetes.test,
                   estimator="BPM",
                   se=TRUE)
#MSE
mean((pred.bas$fit- diabetes.test$y)^2)
[1] 0.4740667
#Coverage
ci.bas = confint(pred.bas)
mean(diabetes.test$y > ci.bas[,1] &
     diabetes.test$y < ci.bas[,2])
[1] 0.98

Theory - Consistency of g-priors

  • desire that posterior probability of model goes to 1 as \(n \to \infty\)

    • does not alwyas hold if the null model is true (may be highest posterior probability model)
    • need prior on \(g\) to depend on \(n\) (rules out EB and fixed g-priors with \(g \ne n\))
    • asymptotically BMA collapses to the true model

  • other quantities may converge i.e. posterior mean

  • what if the true model \(\boldsymbol{\gamma}_T\) is not in \(\Gamma\)? What can we say?

    • \(\boldsymbol{{\cal M}}\)-complete; BMA converges to the model that is “closest” to the truth in Kullback-Leibler divergence
    • \(\boldsymbol{{\cal M}}\)-closed; realize that \((p_\boldsymbol{\gamma}) = 0 \ \forall \boldsymbol{\gamma}\in \mathbf{G}\) and is nonsense but know \(\boldsymbol{\gamma}_T\), however want to use models in \(\mathbf{G}\) only
    • \(\boldsymbol{{\cal M}}\)-open; realize that \((p_\boldsymbol{\gamma}) = 0 \ \forall \boldsymbol{\gamma}\in \mathbf{G}\) and is nonsense but know \(\boldsymbol{\gamma}_T\)
    • latter is related to “stacking” which is a frequentist method of ensemble learning using cross-validation; see Clyde & Iversen (2013) for the curious to motivate via decision theory

Summary

  • Choice of prior on \(\boldsymbol{\beta_\gamma}\)

    • orthogonally invariant priors - multivariate Spike & Slab
    • products of independent Spike & Slab priors
    • non-semi-conjugate

  • priors on the models (sensitivity)

  • computation (MCMC, “stochastic search”, variational, orthogonal data augmentation, reversible jump-MCMC)

  • posterior summaries - select a model or “average” over all models

Other aspects of model selection?

  • transformations of \(\mathbf{Y}\)
  • functions of \(\mathbf{X}\): interactions or nonlinear functions such as splines kernels
  • choice of error distribution