\(h_{ii}\) is the \(i\)th diagonal element of the hat matrix \(\mathbf{H}= \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\) or leverage
Under correct model standardized residuals have mean 0 and scale 1
plug in the usual unbiased estimate of \(\sigma^2\)\[r_i = e_i/\sqrt{\hat{\sigma}^2(1 - h_{ii})}
\]
if \(h_{ii}\) is close to 1, then \(\hat{Y}_i\) is close to \(Y_i\) (why?!?) so \(e_i\) is approximately 0
\(\textsf{var}(e_i)\) is also almost 0 as \(h_{ii} \to 1\), so \(e_i \to 0\) with probability 1
if \(h_{ii} \approx 1\)\(r_i\) may not flag ``outliers’’
even if \(h_{ii}\) is not close to 1, the distribution of \(r_i\) is not a \(t\) (hard to judge if large \(|r_i|\) is unusual)
Outlier Test for Mean Shift
Test \(H_0\): \(\mu_i = \mathbf{x}_i^T \boldsymbol{\beta}\) versus \(H_a\): \(\mu_i = \mathbf{x}_i^T\boldsymbol{\beta}+ \alpha_i\)
t-test for testing H\(_0\): \(\alpha_i = 0\) has \(n - p -1\) degrees of freedom
if p-value is small declare the \(i\)th case to be an outlier: \(\textsf{E}[Y_i]\) not given by \(\mathbf{X}\boldsymbol{\beta}\) but \(\mathbf{X}\boldsymbol{\beta}+ \delta_i \alpha_i\)
Can extend to include multiple \(\delta_i\) and \(\delta_j\) to test that case \(i\) and \(j\) are both outliers
Extreme case \(\boldsymbol{\mu}= \mathbf{X}\boldsymbol{\beta}+ \mathbf{I}_n \boldsymbol{\alpha}\) all points have their own mean!
Need to control for multiple testing without prior reason to expect a case to be an outlier (or use a Bayesian approach)
standardized predicted residual is \[\frac{e_{(i)}}{\sqrt{\textsf{var}(e_{(i)})}} = \frac{e_i/(1 -
h_{ii})}{\sigma/\sqrt{1 - h_{ii}}} = \frac{e_i}{\sigma \sqrt{1 -
h_{ii}} }
\]
these are the same as standardized residual!
How to Calculate \(\hat{\boldsymbol{\beta}}_{(i)}\)
How do we calculate \(\hat{\boldsymbol{\beta}}_{(i)}\) without case \(i\) without refitting the model \(n\) times?
Note: \(\mathbf{X}^T\mathbf{X}= \mathbf{X}_{(i)}^T\mathbf{X}_{(i)} + \mathbf{x}_i\mathbf{x}_i^T\) rearrange to get \(\mathbf{X}_{(i)}^T\mathbf{X}_{(i)} = \mathbf{X}^T\mathbf{X}- \mathbf{x}_i\mathbf{x}_i^T\)
Special Case of Binomial Inverse Theorem or Woodbury Theorem: (Thm B.56 in Christensen) \[(\mathbf{A}+ \mathbf{u}\mathbf{v}^T)^{-1} = \mathbf{A}^{-1} - \frac{\mathbf{A}^{-1} \mathbf{u}\mathbf{v}^T \mathbf{A}^{-1}}{1 + \mathbf{v}^T \mathbf{A}^{-1} \mathbf{u}}\] with \(\mathbf{A}= \mathbf{X}^T\mathbf{X}\) and \(\mathbf{u}= -\mathbf{x}_i\) and \(\mathbf{v}= \mathbf{x}_i\)
\[(\mathbf{X}_{(i)}^T\mathbf{X}_{(i)})^{-1} = (\mathbf{X}^T\mathbf{X}- \mathbf{x}_i\mathbf{x}_i^T)^{-1} = (\mathbf{X}^T\mathbf{X})^{-1} + \frac{(\mathbf{X}^T\mathbf{X})^{-1} \mathbf{x}_i \mathbf{x}_i^T (\mathbf{X}^T\mathbf{X})^{-1}}{1 - \mathbf{x}_i^T (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{x}_i}\] - use \(\mathbf{X}_{i}^T\mathbf{Y}_{i} = \mathbf{X}^T\mathbf{Y}- \mathbf{x}_i y_i\) to get \(\hat{\boldsymbol{\beta}}_{(i)}\) and other quantities
External estimate of \(\sigma^2\)
Estimate \({\hat{\sigma}}^2_{(i)}\) using data with case \(i\) deleted \[\begin{eqnarray*}
\textsf{SSE}_{(i)} & = & \textsf{SSE}- \frac{e_i^2}{1 - h_{ii}} \\
{\hat{\sigma}}^2_{(i)} = \textsf{MSE}_{(i)} & = & \frac{\textsf{SSE}_{(i)}}{n - p - 1} \\
\end{eqnarray*}\]
Externally Standardized residuals \[t_i = \frac{e_{(i)}}{\sqrt{{\hat{\sigma}}^2_{(i)}/(1 - h_{ii})}} = \frac{y_i
- \mathbf{x}_i^T \hat{\boldsymbol{\beta}}_{(i)}} {\sqrt{{\hat{\sigma}}^2_{(i)}/(1 - h_{ii})}} = r_i \left(
\frac{ n - p - 1}{n - p - r_i^2}\right)^{1/2}\]
May still miss extreme points with high leverage, but will pick up unusual \(y_i\)’s
Externally Studentized Residual
Externally studentized residuals have a \(t\) distribution with \(n - p - 1\) degrees of freedom: \[t_i = \frac{e_{(i)}}{\sqrt{{\hat{\sigma}}^2_{(i)}/(1 - h_{ii})}} = \frac{y_i
- \mathbf{x}_i^T \hat{\boldsymbol{\beta}}_{(i)}} {\sqrt{{\hat{\sigma}}^2_{(i)}/(1 - h_{ii})}} \sim \textsf{St}(n - p - 1)\] under the hypothesis that the \(i\)th case is not an “outlier”.
This externally studentized residual statistic is equivalent to the t-statistic for testing that \(\alpha_i\) is zero!
(HW)
Multiple Testing
without prior reason to suspect an outlier, usually look at the maximum of the \(|t_i|\)’s
is the \(\max |t_i|\) larger than expected under the null of no outliers?
Need distribution of the max of Student \(t\) random variables (simulation?)
a conservative approach is the Bonferroni Correction: For \(n\) tests of size \(\alpha\) the probability of falsely labeling at least one case as an outlier is no greater than \(n \alpha\); e.g. with 21 cases and \(\alpha = 0.05\), the probability is no greater than 1.05!
adjust \(\alpha^* = \alpha/n\) so that the probability of falsely labeling at least one point an outlier is \(\alpha\)
with 21 cases and \(\alpha = 0.05\), \(\alpha/n = .00238\) so use \(\alpha^* = 0.0024\) for each test
Influence - Cook’s Distance
Cook’s Distance measure of how much predictions change with \(i\)th case deleted \[\begin{eqnarray*}
D_i & = &\frac{\| \hat{\mathbf{Y}}_{(i)} - \hat{\mathbf{Y}} \|^2}{ p {\hat{\sigma}}^2} =
\frac{ (\hat{\boldsymbol{\beta}}_{(i)} - \hat{\boldsymbol{\beta}})^T \mathbf{X}^T\mathbf{X}(\hat{\boldsymbol{\beta}}_{(i)} - \hat{\boldsymbol{\beta}}) }{ p
{\hat{\sigma}}^2} \\
& = & \frac{r_i^2}{p} \frac{h_{ii}}{ 1 - h_{ii}}
\end{eqnarray*}\]
Flag cases where \(D_i > 1\) or large relative to other cases
Influential Cases are those with extreme leverage or large \(r_i^2\)
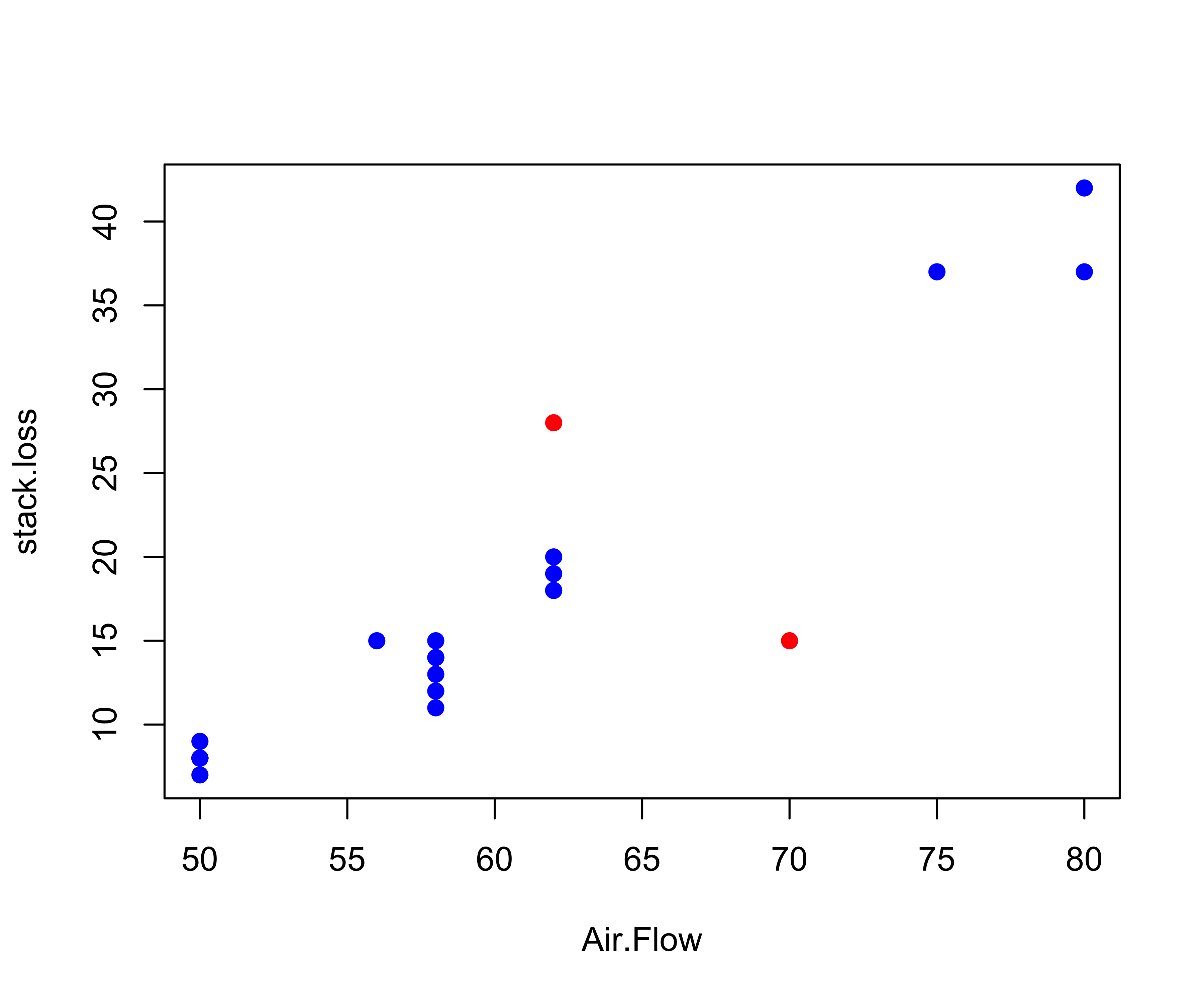
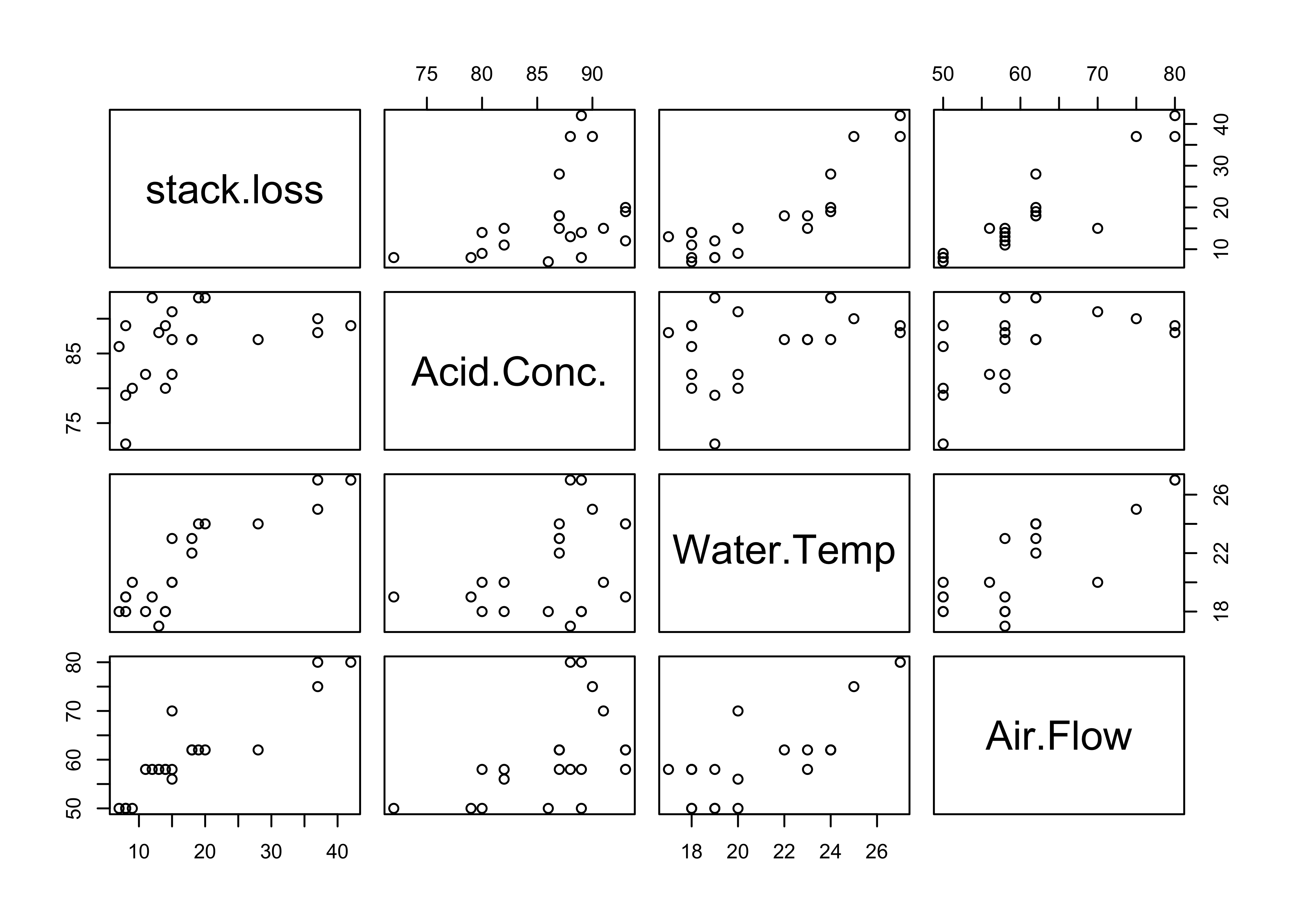
Stackloss Data
Case 21
Leverage \(0.285\) (compare to \(p/n = .19\) )
p-value \(t_{21}\) is \(0.0042\)
Bonferroni adjusted p-value is \(0.0024\) (not really an outlier?)
Cooks’ Distance \(.69\)
Other points? Masking?
Refit without Case 21 and compare results
Other analyses have suggested that cases (1, 2, 3, 4, 21) are outliers
provides an approach to identify outliers or surprising variables by looking at the probabilty that the error for a case is more than \(k\) standard deviations above or below zero. \[P(|\epsilon_i| > k \sigma \mid \mathbf{Y})\]
Cases with a high probability (absolute fixed value of \(k\) or relative to a multiplicity correction to determine \(k\)) are then investigated.
find posterior distribution of \(\epsilon_i\) given the data and model
Chaloner and Brant use a reference prior for the analysis \(p(\boldsymbol{\beta}, \phi) \propto 1/\phi\)
no closed form solution for the probability but can be approximated by MCMC or a one dimensional integral! see ?BAS::Bayes.outlier
Stackloss Data
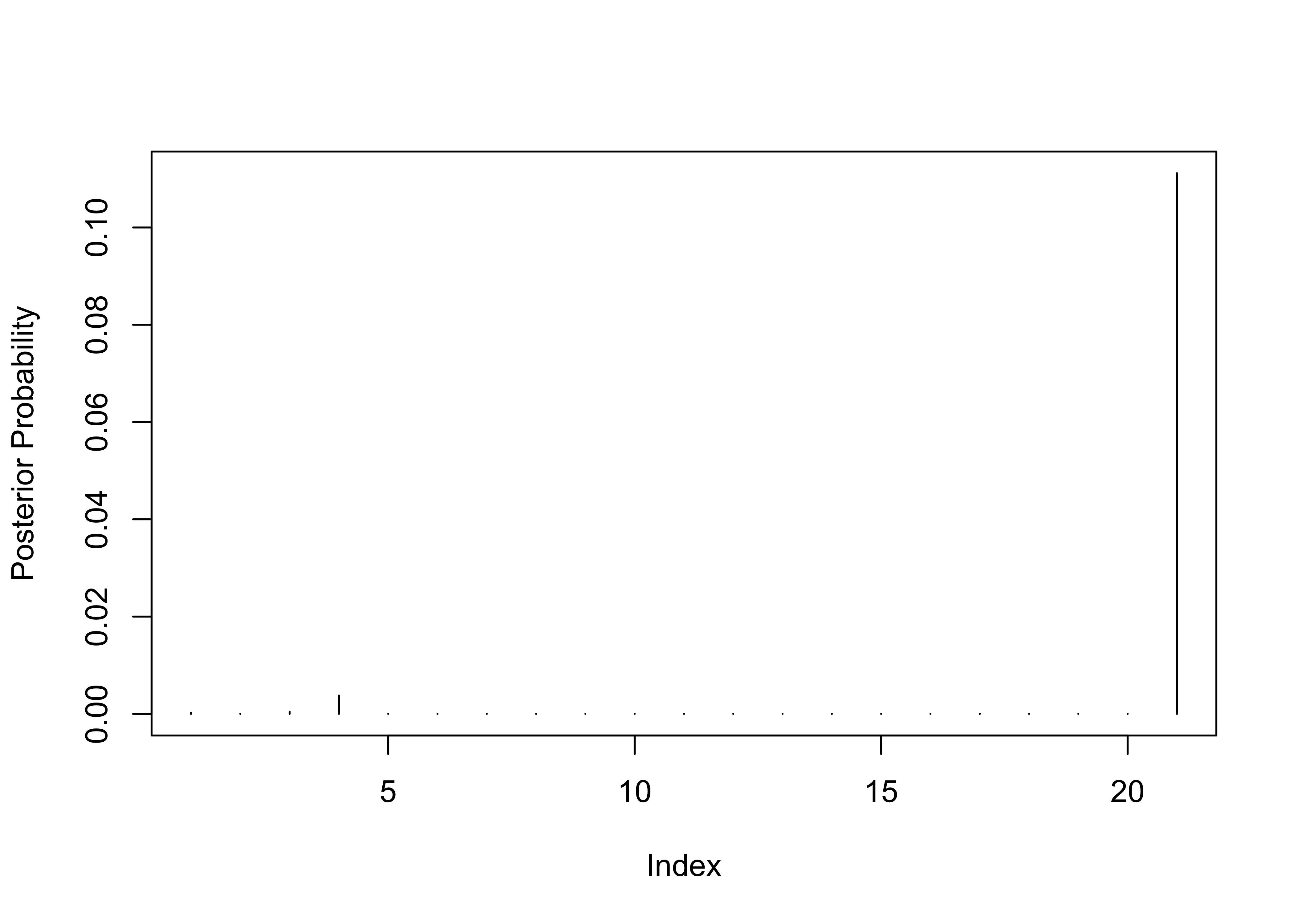
library(BAS)stack.lm <-lm(stack.loss ~ ., data = stackloss)stack.outliers <- BAS::Bayes.outlier(stack.lm, k =3)plot(stack.outliers$prob.outlier, type ="h", ylab ="Posterior Probability")
Stackloss Data
Adjust prior probability for multiple testing with sample size of 21 and prior probability of no outliers 0.95
