Transformations and Normality Assumptions

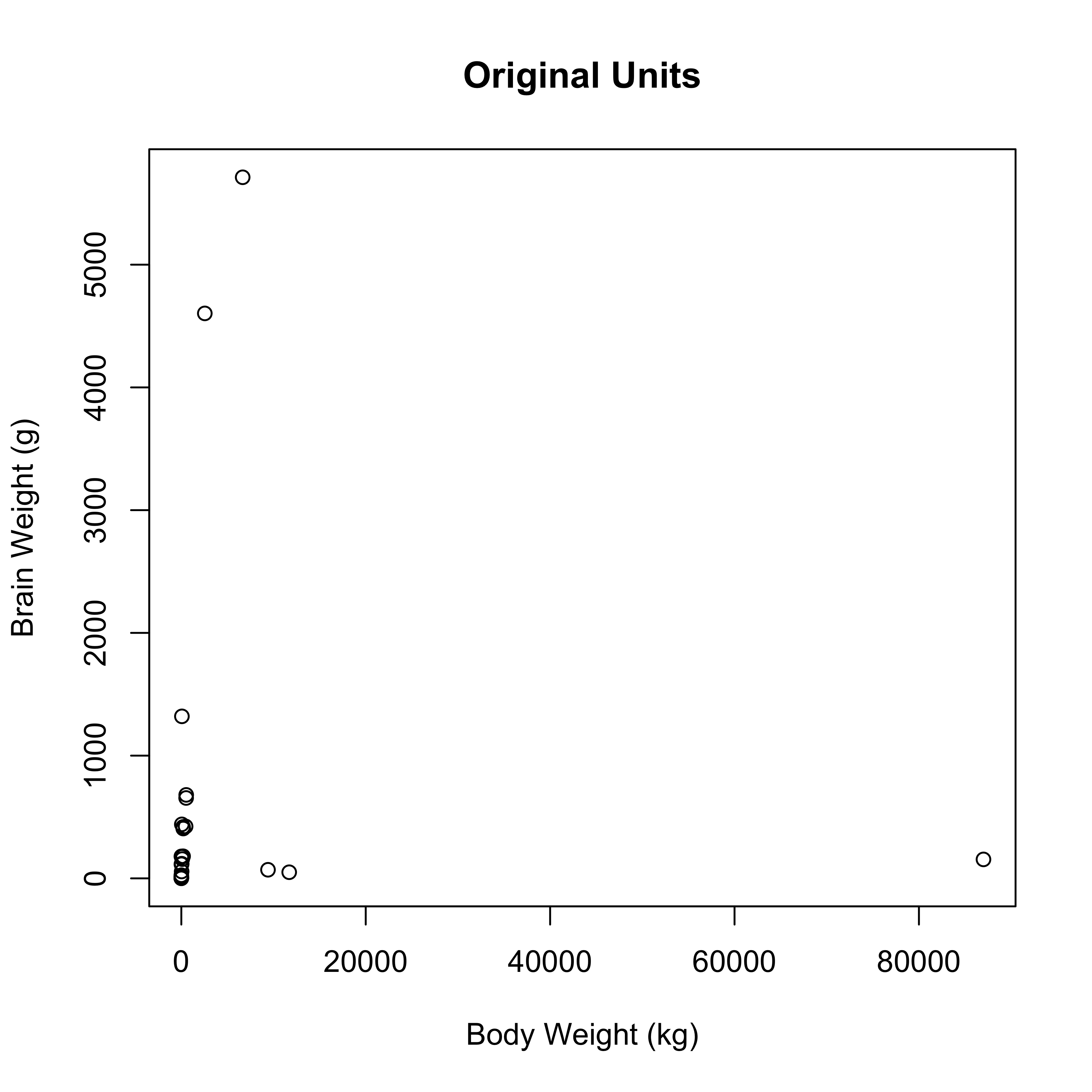
STA 721: Lecture 22

Merlise Clyde

Duke University

Outline

• Normality & Transformations
• Box-Cox
• Variance Stabilizing Transformations
• Nonlinear Regression

Readings: Christensen Chapter 13, Seber & Lee Chapter 10 & Wakefield Chapter 6

Model Assumptions

Linear Model: \[ \mathbf{Y}= \boldsymbol{\mu}+ \boldsymbol{\epsilon}\]
Assumptions:
\[\begin{eqnarray*} \boldsymbol{\mu}\in C(\mathbf{X}) & \Leftrightarrow & \boldsymbol{\mu}= \mathbf{X}\boldsymbol{\beta}\\ \boldsymbol{\epsilon}& \sim & \textsf{N}(\mathbf{0}_n, \sigma^2 \mathbf{I}_n) \end{eqnarray*}\]

• Normal Distribution for \(\mathbf{Y}\) with constant variance or fixed covariance
• linearity of \(\boldsymbol{\mu}\) in \(\mathbf{X}\)
• Computational Advantages of Normal Models
• Robustify with heavy tailed error distributions

Checking via QQ-Plots

• QQ-Plots are a graphical tool to assess normality

• Order residuals \(e_i\): \(e_{(1)} \le e_{(2)} \ldots \le e_{(n)}\) sample order statistics or sample quantiles (standardized - divide by \(\sqrt{1 - h_{ii}}\)

• Let \(z_{(1)} \le z_{(2)} \ldots z_{(n)}\) denote the expected order statistics of a sample of size \(n\) from a standard normal distribution ``theoretical quantiles’’
  

• If the \(e_i\) are normal then \(\textsf{E}[e_{(i)}/\sqrt{1 - h_{ii}}] = \sigma z_{(i)}\)
  

• Expect that points in a scatter plot of \(e_{(i)}/\sqrt{1 - h_{ii}}\) and \(z_{(i)}\) should be on a straight line.
  

• Judgment call - use simulations to gain experience!

Animal Example

data(Animals, package="MASS")
plot(brain ~ body, data=Animals, xlab="Body Weight (kg)", ylab="Brain Weight (g)", main="Original Units")

Residual Plots

brains.lm <- lm(brain ~ body, data=Animals)
par(mfrow=c(2,2))
plot(brains.lm)

Normality Assumption

Recall:

\[\begin{eqnarray*} \mathbf{e}& = &(\mathbf{I}- \mathbf{P}_\mathbf{X}) \mathbf{Y}\\ & = & (\mathbf{I}- \mathbf{P}_\mathbf{X})(\mathbf{X}\hat{\boldsymbol{\beta}}+ \boldsymbol{\epsilon}) \\ & = & (\mathbf{I}- \mathbf{P}_\mathbf{X})\boldsymbol{\epsilon} \end{eqnarray*}\]

\[e_i = \epsilon_i - \sum_{j=1}^n h_{ij} \epsilon_j\]

• Lyapunov CLT (independent but not identically distributed) implies that residuals will be approximately normal (even for modest \(n\)), if the errors are not normal

• Supernormality of residuals

• clearly not the case here!

Box-Cox Transformation

Box and Cox (1964) suggested a family of power transformations for \(Y > 0\)
\[ U(\mathbf{Y}, \lambda) = Y^{(\lambda)} = \left\{ \begin{array}{ll} \frac{(Y^\lambda -1)}{\lambda} & \lambda \neq 0 \\ \log(Y) & \lambda = 0 \end{array} \right. \]

• Estimate \(\lambda\) by maximum Likelihood
  \[{\cal{L}}(\lambda, \boldsymbol{\beta}, \sigma^2) \propto \prod f(y_i \mid \lambda, \boldsymbol{\beta}, \sigma^2)\]

• \(U(\mathbf{Y}, \lambda) = Y^{(\lambda)} \sim \textsf{N}(\mathbf{X}\boldsymbol{\beta}, \sigma^2)\)

• Jacobian term is \(\prod_i y_i^{\lambda - 1}\) for all \(\lambda\)
  

• Profile Likelihood based on substituting MLE \(\boldsymbol{\beta}\) and \(\sigma^2\) for each value of \(\lambda\) is \[\log({\cal{L}}(\lambda) \propto (\lambda -1) \sum_i \log(Y_i) - \frac{n}{2} \log(\textsf{SSE}(\lambda))\]

Profile Likelihood

• Profile Likelihood is a function of \(\lambda\) obtained by substituting the MLE of \(\boldsymbol{\beta}\) and \(\sigma^2\) for each value of \(\lambda\)

MASS::boxcox(brains.lm, lambda=seq(-2, 2, by=0.1))

Residuals after Transformation of Response

plot(lm(log(brain) ~ body, data=Animals))

Residuals after Transformation of Response and Predictor

logbrain.lm <- lm(log(brain) ~ log(body), data=Animals)
plot(logbrain.lm)

Transformed Data

plot(brain ~ body, data=Animals, xlab="Body Weight (kg)", ylab="Brain Weight (g)", log="xy", main="Logarithmic Scale")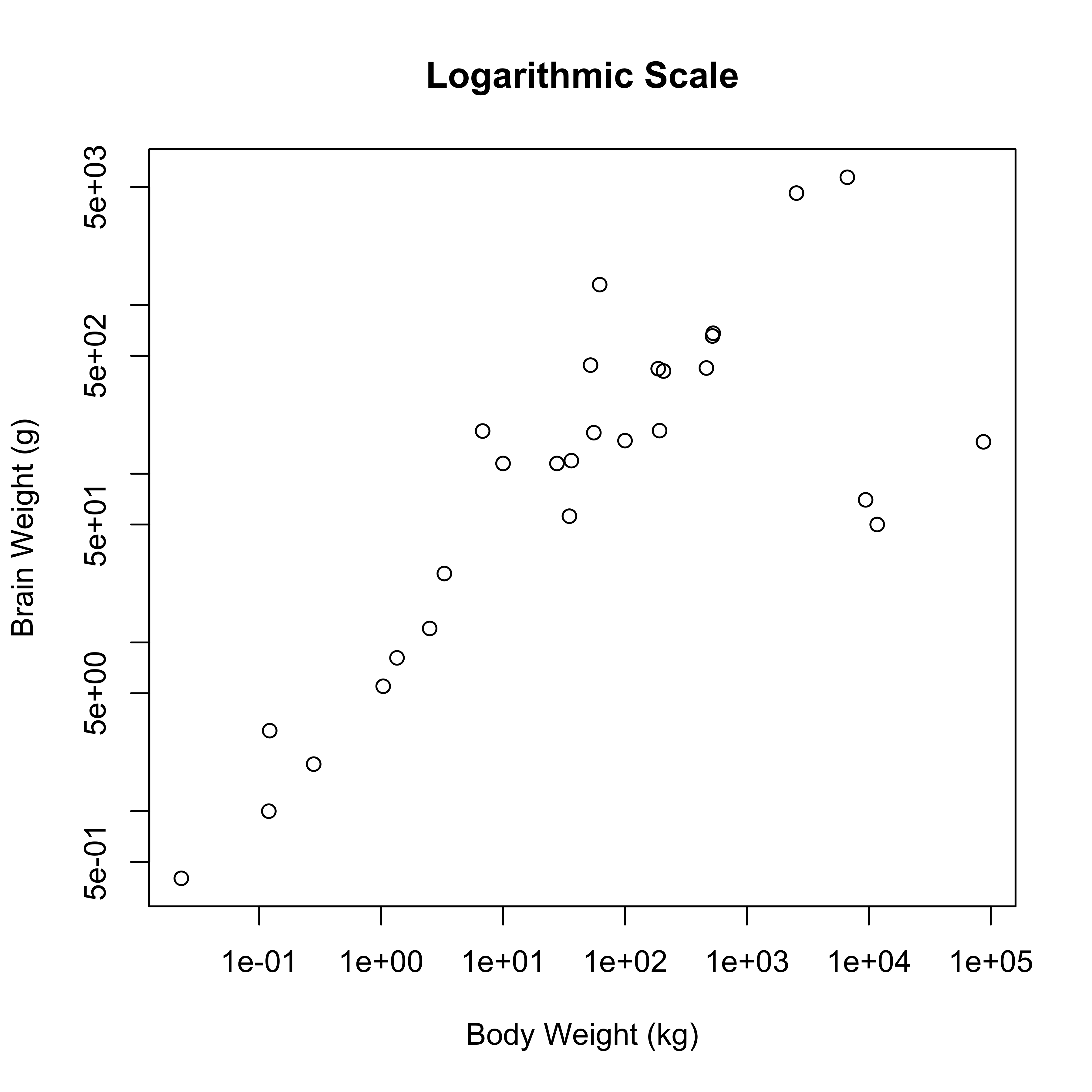

Test that Dinosaurs are from a Different Population (outliers)

logbrains.nodino.lm = lm(log(brain) ~ log(body) + 
                           I(row.names(Animals) == "Triceratops") +  
                           I(row.names(Animals) == "Brachiosaurus") + 
                           I(row.names(Animals) == "Dipliodocus"), 
                         data=Animals)

anova(logbrain.lm, logbrains.nodino.lm)

Analysis of Variance Table

Model 1: log(brain) ~ log(body)
Model 2: log(brain) ~ log(body) + I(row.names(Animals) == "Triceratops") + 
    I(row.names(Animals) == "Brachiosaurus") + I(row.names(Animals) == 
    "Dipliodocus")
  Res.Df    RSS Df Sum of Sq     F    Pr(>F)
1     26 60.988                             
2     23 12.117  3    48.871 30.92 3.031e-08

Animals = cbind(Animals, diag(28)); colnames(Animals)[3:30] = rownames(Animals)
brains.bas = bas.lm(log(brain) ~ log(body) + . - body, data=Animals, 
                    prior="hyper-g-n", a=3,modelprior=beta.binomial(1,28), method="MCMC", n.models=10000, MCMC.it=2^17)
image(brains.bas, rotate=FALSE)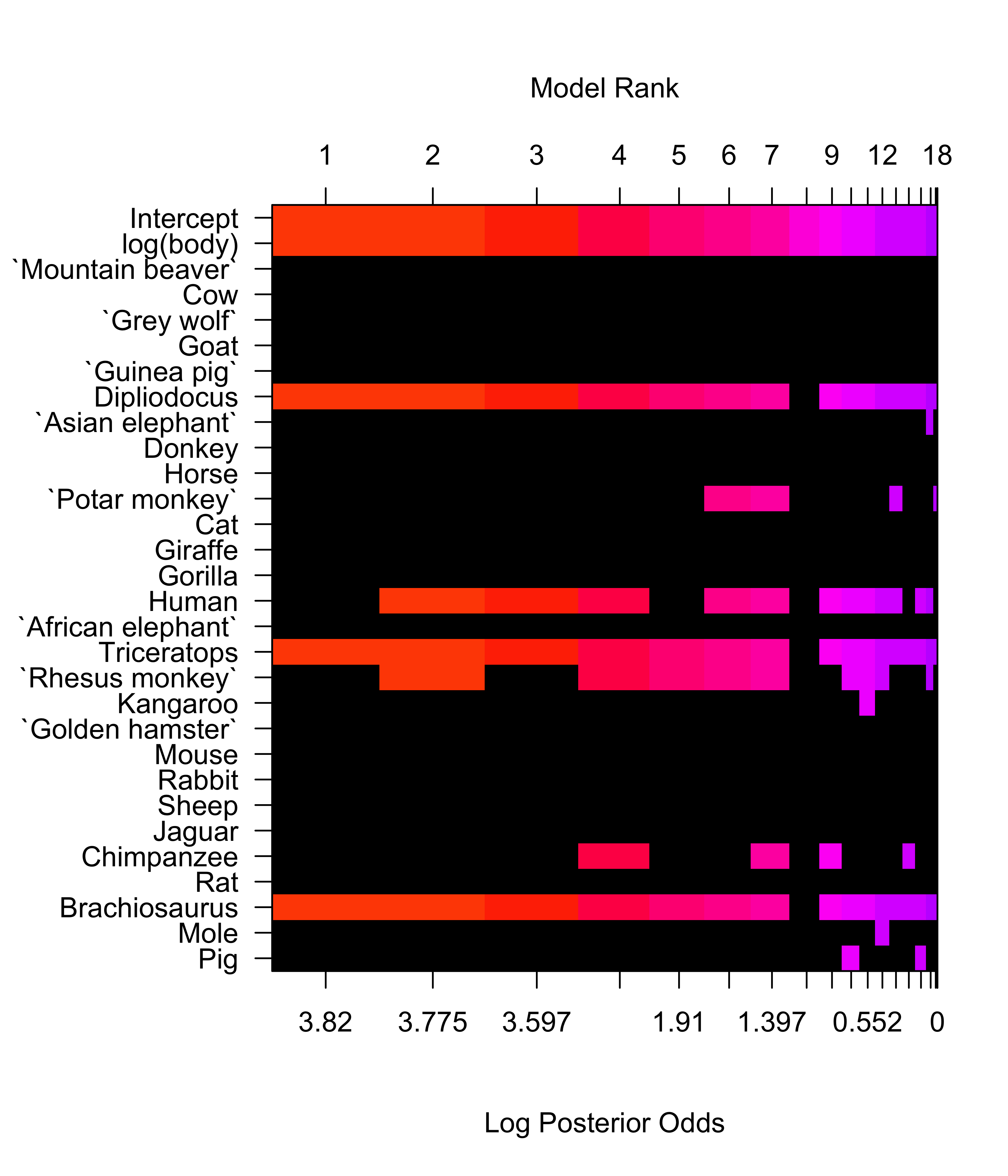

Variance Stabilizing Transformations

• If \(Y - \mu\) (approximately) \(N(0, h(\mu))\)

• Delta Method implies that \[g(Y) \stackrel{\cdot}{\sim}\textsf{N}( g(\mu), g'(\mu)^2 h(\mu))\]

• Find function \(g\) such that \(g'(\mu)^2 h(\mu)\) is constant \[g(Y) \sim N(g(\mu), c)\]

• Poisson Counts (need \(Y > 3\)), \(g\) is the square root transformation

• Binomial: \(\arcsin(\sqrt{Y})\)

Note: transformation for normality may not be the same as the variance stabilizing transformation; boxcox assumes mean function is correct

Generalized Linear Models are preferable to transforming data, but may still be useful for starting values for MCMC

Nonlinear Regression

• Drug concentration of caldralazine at time \(X_i\) in a cardiac failure patient given a single 30mg dose \((D = 30)\) given by \[ \mu(\boldsymbol{\beta}) = \left[\frac{D}{V} \exp(-\kappa_e x_i) \right] \] with \(\boldsymbol{\beta}= (V, \kappa_e)\) \(V = volume\) and \(\kappa_e\) is the elimination rate

• If \(Y_i = \left[\frac{D}{V} \exp(-\kappa_e x_i) \right] \times \epsilon_i\) with \(\log(\epsilon_i) \mathrel{\mathop{\sim}\limits^{\rm iid}} N(0, \sigma^2)\) then the model is intrinisically linear (can transform to linear model)

\[\begin{eqnarray*} \log(\mu(\boldsymbol{\beta})) & = & \log\left[\frac{D}{V} \exp(-\kappa_e x_i) \right] = \log[D] - \log(V) -\kappa_e x_i \\ log(Y_i) - \log[30] & = &\beta_0 + \beta_1 x_i + \epsilon_i \end{eqnarray*}\] where \(\epsilon_i\) has a log normal distribution

Nonlinear Least Squares Example

x = c(2,4,6,8,10,24,28, 32)
y = c(1.63, 1.01, .73, .55, .41, .01, .06, .02)

conc.lm = lm(I(log(y) - log(30)) ~ x)

vhat = exp(-coef(conc.lm)[1])
khat = -coef(conc.lm)[2]

vhat

(Intercept) 
   16.66331 

khat

        x 
0.1521064 

plot(x, y)
lines(x, (30/vhat)*exp(-khat*x))

Additive Error Model

• If \(\mathbf{Y}= \left[\frac{D}{V} \exp(-\kappa_e x_i) \right] + \epsilon_i\) model is intrinisically nonlinear and cannot transform to a linear model.

• need to use nonlinear least squares to estimate \(\boldsymbol{\beta}\) and \(\sigma^2\)

• or MCMC to estimate the posterior distribution of \(\boldsymbol{\beta}\) and \(\sigma^2\)

Intrinsically Linear Model nls

df = data.frame(y=y, x=x)
logconc.nlm = nls( log(y) ~ log((30/V)*exp(-k*x)), data=df, start=list(V=vhat, k=khat))
summary(logconc.nlm)

Formula: log(y) ~ log((30/V) * exp(-k * x))

Parameters:
              Estimate Std. Error t value Pr(>|t|)
V.(Intercept) 16.66331    7.11923   2.341 0.057796
k.x            0.15211    0.02368   6.423 0.000673

Residual standard error: 0.7411 on 6 degrees of freedom

Number of iterations to convergence: 0 
Achieved convergence tolerance: 4.056e-09

Intrinsically Nonlinear Model

Formula: y ~ (30/V) * exp(-k * x)

Parameters:
  Estimate Std. Error t value Pr(>|t|)
V 13.06506    0.60899   21.45 6.69e-07
k  0.18572    0.01124   16.52 3.14e-06

Residual standard error: 0.05126 on 6 degrees of freedom

Number of iterations to convergence: 4 
Achieved convergence tolerance: 7.698e-06

Functions of Interest

Interest is in

• clearance: \(V \kappa_e\)

• elimination half-life \(x_{1/2} = \log 2/\kappa_e\)

• Use properties of MLEs: asymptotically \(\hat{\boldsymbol{\beta}} \sim N\left(\boldsymbol{\beta}, I(\hat{\boldsymbol{\beta}})^{-1}\right)\)

• Asymptotic Distributions

• Bayes obtain the posterior directly for parameters and functions of parameters!

  • Priors?
  • Constraints on Distributions?
  • Bayes Factor for testing normal vs log-normal models?

Summary

• Optimal transformation for normality (MLE) depends on choice of mean function
• May not be the same as the variance stabilizing transformation
• Nonlinear Models as suggested by Theory or Generalized Linear Models are alternatives
• ``normal’’ estimates may be useful approximations for large \(p\) or for starting values for more complex models (where convergence may be sensitive to starting values)